Numeracy is the foundation of mathematics learning. It’s more than just being able to calculate—it’s the ability to think flexibly with numbers, recognize patterns, and solve problems using efficient strategies. In K–12 classrooms, building strong numeracy skills early leads to greater success in higher-level math.
Why Numeracy Is Important
Numeracy is not just a math skill—it’s a life skill. Students with strong numeracy can:
- Approach unfamiliar problems with confidence and flexibility.
- Recognize relationships and patterns between numbers and select efficient strategies to solve problems.
- Transfer mathematical understanding to other subjects, like science, technology, and even language arts, when analyzing data or patterns.
Conversely, students who lack numeracy often rely solely on memorized procedures or make careless mistakes. When problems look different from what they have practiced, they can become stuck and frustrated. By focusing on building numeracy, teachers help students develop the confidence, adaptability, and critical thinking skills that extend beyond the math classroom.
What is FLEXIBILITY?
Flexibility with numbers means that a student can think about a problem in a variety of ways. Here is an example:

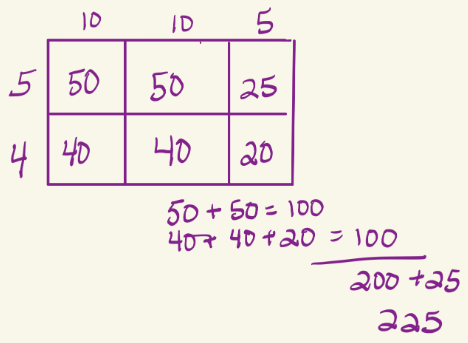
How many of your students would ONLY know to do this?

This algorithmic method does not honor place value, which can diminish a student’s understanding of numeracy.
While using a standard algorithm is ONE way to solve this problem, we want students to be flexible in their thinking. Therefore, we want to always highlight a variety of student thinking. You are not showing students 5 ways to do a problem; rather, you are encouraging students to always think of 2 ways to do the problem. Then you ask STUDENTS to share their thinking, and you highlight creative thinking. Students will begin to understand that creative, numeric thinking gets the high five!
Number Talks in the Classroom: Building Number Sense Through Conversation
Number Talks are short, daily math discussions—usually 5 minutes—designed to develop number sense and computational flexibility. In a Number Talk, students solve a problem mentally, share their thinking, and learn new strategies from their peers. Teachers can also use images to spark mathematical conversations that build numeracy skills. Kristen Acosta Number Talk Images
For example, for 36 + 49, one student might think: “Add 6 to 49 to get 55, then add 30 to make 85.” Another might add 30 + 40 = 70, then 6 + 9 = 15, and combine for 85. Hearing multiple approaches helps all students expand their mental math toolbox. Using visual models, such as a number line, can support students who struggle to visualize mathematics.

Daily Number Talks don’t just improve computation—they also build a classroom culture where mathematical thinking is valued over speed and memorization.
Check out my blog on Number Talk model dialogues
Check out my Numeracy Resource Folders for access to daily number talk slides and other fantastic numeracy activities to use in your classroom.
Numeracy-Based Computation Strategies: Going Beyond Memorized Steps
Strong numeracy requires more than mastering standard algorithms. Students need numeracy-based computation strategies that make numbers meaningful and flexible.
Some effective numeracy strategies include:
- Decomposing numbers: Break numbers into parts based on place value.
Example: 47 + 36 = (40 + 30) + (7 + 6) = 70 + 13 = 83. - Compensation: Adjust numbers to make the math easier.
Example: 59 + 38 → 60 + 37 = 97. - Friendly numbers: Use numbers ending in zeros or multiples of ten.
- Doubling and halving: For multiplication, 25 × 16 = 50 × 8 = 400.
- Partial products/partial quotients: Break multiplication or division into smaller, easier steps.


When students understand these strategies, they are better able to select the most efficient method for a problem, leading to greater accuracy and independence.
Math Manipulatives and Visual Models: Making Learning Concrete
Math manipulatives and visual models are essential tools for building numeracy because they make abstract concepts visible and tangible. When students can touch, move, and see mathematics, they develop deeper conceptual understanding.
Examples include:
- Base-ten blocks for place value and regrouping:
In a second-grade classroom, students use base-ten blocks to solve 235 – 178. They physically trade one hundred blocks for ten tens and then regroup a ten into ten ones, seeing why the subtraction algorithm works instead of memorizing “borrow and subtract.”

- 10×10 grids for operations, fractions, and decimals:
In a fifth-grade lesson on adding decimals, students shaded .6 and 0.75 on a 10 x 10 grid. This allows students to visually ‘see’ how large the sum will be.
- Fraction strips or tiles for equivalence and comparison:
In fourth grade, students compare 2/3 and 3/5 by laying fraction strips side-by-side, noticing that ⅔ is longer than 3/5. This concrete comparison supports fraction reasoning before moving to common denominators symbolically.
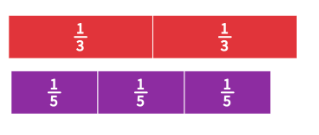
Fraction strips or tiles for equivalence and comparison
- Rekenreks for early number sense:
In a first-grade Number Talk, students use a rekenrek to show 8 + 5. One student slides 2 beads to complete a ten on the top row and explains, “I made 10 and then added 3 more to get 13.” This supports the make-a-ten strategy.
- Two-color counters for integer operations:
In a seventh-grade class, students working with integers use counters—red for negatives, yellow for positives—to model (–3 + 5), pairing and removing zero pairs until only two positive counters remain.
Research supports the use of manipulatives not just for early grades but across K–12. They help correct misconceptions, support diverse learners, and bridge the gap from concrete understanding to symbolic representation. In classrooms where manipulatives are embedded into daily instruction, students not only “get the right answer” but can explain why it works.
Final Thoughts
Numeracy is the heartbeat of mathematical success. Without it, students may perform procedures but lack the understanding needed to apply math flexibly. With it, they gain the tools to tackle any mathematical situation—inside or outside the classroom.
Number Talks build mathematical conversation and strategic thinking. Reasoning-based computation strategies help students think beyond memorized steps. Math manipulatives and visual models make abstract ideas accessible for all learners.
When K–8 teachers intentionally embed these strategies into daily instruction, they empower students to become confident, capable, and curious mathematical thinkers—ready for the challenges of both higher mathematics and the real world.
